For whatever reason, one of my projects at my current employer led me to a need for doing some 3D work in HTML5′s canvas element. After a few hack-ish, amateur attempts at repurposing what I’d done for Mega Hovertank Wars, I decided to use something with a community behind it and found three.js from Mr.doob, a man you may have heard of through his work on Arcade Fire’s HTML5 experiment “The Wilderness Downtown.” There are plenty of other options out there (including some that use WebGL rather than a pure canvas renderer), but I think after perusing its examples and reading Seb Lee-Delisle’s blog, I’d settled on three.js.

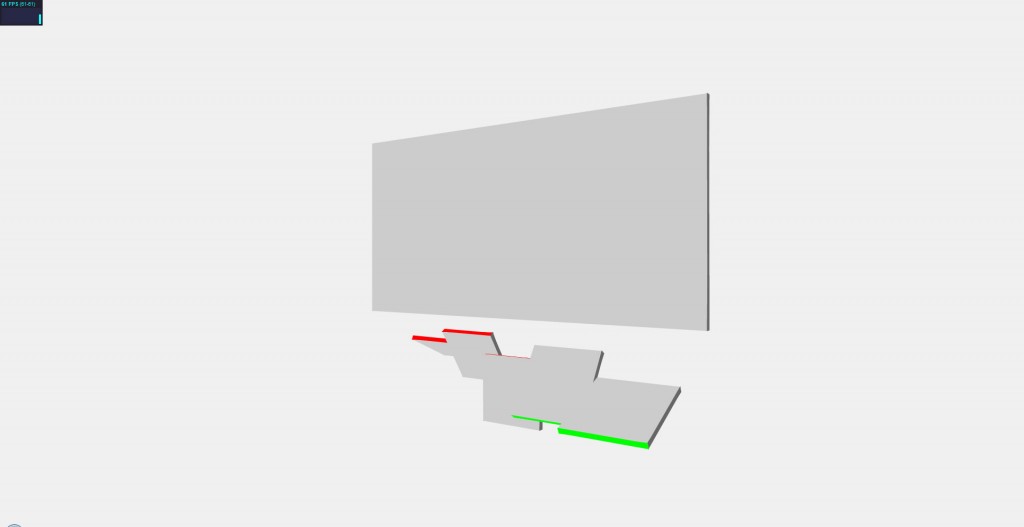
By modifying the geometry_cube.html example, I arrived at this:

All I did was change the face materials of the starting cube and used that materials array to color the 5 flaps below (along with changing some Camera() and Cube() dimension and position parameters, but those are pretty obvious):

That was the simple part. The only true oddity is setting the autoUpdateMatrix attribute of each square to false. This is because if you don’t do this, you can’t manually modify each square’s matrix later on. Also, if you notice, when you drag around on the example, the cube spins, and I wanted to incorporate that into the “flaps” animations.

Relative Animation

Well, that’s what I’m calling it anyways. What it really means is that I based the “flapping” intensity on the difference between the main panel’s targetRotation and current rotation (cube.rotation.y).

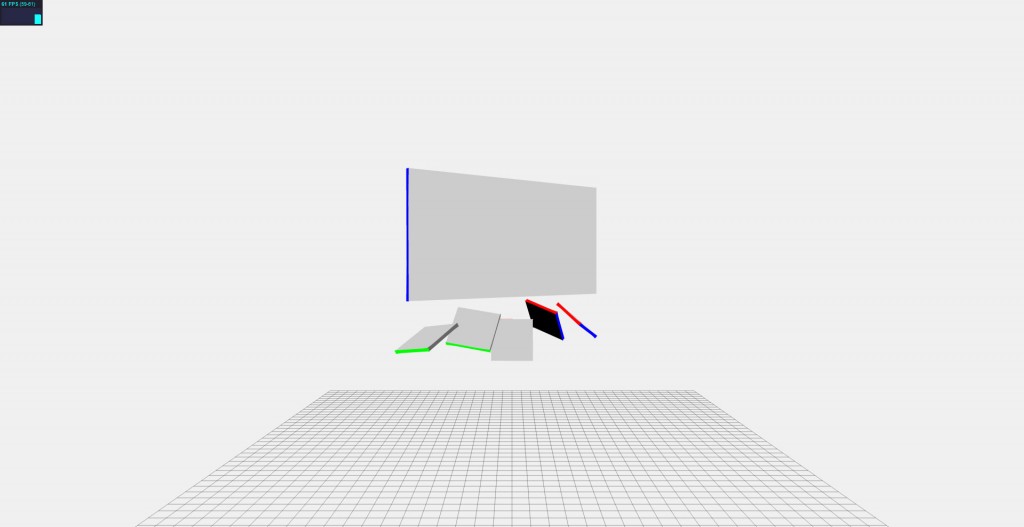
The physics I was hoping to achieve was something that looked like there is a rope between the panel and the squares and they flail in the wind behind the panel as it rotates. Something like this:

It looks pretty good considering the code is based mostly on basic advanced math.

The first key is that in the lines where I’m setting each flap’s position.y, position.x and position.z values, that is to give the “roped” effect. All I’m really doing is adding to each position coordinate as if it were rotating on a hinge. Simple math!

The second key is that you are determining the vector pointing along the front face of the panel at any given point of the rotation by taking the Math.cos() and Math.sin() values of the current rotational value of the panel. This allows us to find the axis we need to rotate each square.

3D Rotation Along An Arbitrary Axis

However, doing this was harder than I thought it would be. After some quick Googling, however, I found an extremely helpful Stack Overflow post and simply adapted some of the help in the discussion for my own purposes:

To simplify, you want to find the axis and angle that will get the original vector to match the desired vector, cross-multiply them, and normalize. That will allow you to form the rotation and revolution matrices which you can then multiply with the position matrix (the ordering of which is important, i.e. (revolve x rotate) x position) which results in the final position and orientation matrix.

Integrating JigLibJS Physics

Unfortunately, this wasn’t as realistic as I’d hoped. I could have done more tweaking to avoid some faults against true physics (such as when you abruptly change directions but only to stop rotation, the squares don’t swing back and forth in a natural fashion), but the end goal for this little side project was much more grand to the point where it just made more sense to use real physics.

Always interested by physics engines such as Havok, a popular choice for video game developers, I started to browse. I first arrived at a port of the Bullet Physics Library for JavaScript by Pl4n3, but it was incredibly buggy. Object would collide and bounce and almost always freeze. I love the effort, but bullet.js was a definite no-go.

Remembering a physics library called JigLib that was ported to Flash from Java, I hoped that someone had done the same for JavaScript, and luckily someone had! JigLibJS was functional, actively developed, and—most importantly—stable.

If you’re not aware (and I wasn’t prior to this little excursion, though in hindsight, it makes total sense), physics engines work by pretty much having you define objects from your rendered model world in the physics world. You then access the objects in the physics engine and take their position and orientations and apply them to the rendering engine, so this is what I did.

JigLibJS is pretty intuitive. The first two lines are system-wide parameters in that everything works on a -9.8 units per second per second gravity and uses the accumulated solver type (it’s the most accurate but is also the slowest of the three).

JigLibJS automatically considers JPlane() objects to be immovable and can thus easily be added to be ground and wall boundaries in the physics system. Other items like boxes are defined and moved about in a manner similar to three.js, so that was handy. One key line for the panel variable is the set_movable(false) so that it isn’t not going to move about under gravity or as other JigLibJS objects collide with it.

I simply repeated that for each square that I wanted and voila, an accurate representation of my models in JigLibJS!

Putting three.js and JigLibJS Together

At this point it was really just taking one matrix (from JigLibJS) and setting the three.js matrix to it. The only weird thing is that I chose to orient the JigLibJS representation of the panel to the three.js representation while the squares went the other way around, i.e. from three.js to JigLibJS. This becomes clear later when I do the world constraints.

It’s very similar to the alignCube() function we had before, except the trouble of turning an axis and an angle into a matrix is done for us prior by JigLibJS. The result is some square falling from underneath the panel and laying there. Exciting, right?

But remember? I want them to hang like they’re on ropes, not fall straight to the ground!

JigLibJS Constraints

Luckily, JigLibJS has these things called constraints. The unfortunate thing is that they don’t work exactly as you would imagine. Whereas the JConstraintMaxDistance seems like it should work (or even the JConstraintPoint), they both have a slight…elasticity to their constraining action and it can’t really be avoided. I even tried out the spring simulation solution, but, surprise surprise, it behaved more like a spring than a rope.

Instead, I used JConstraintWorldPoint. It still has a slight stretch to the constraint distance, but it holds pretty well so long as you don’t spin the panel too fast.

This little piece of code was simply added into the loop I had going for when I was creating each square in JigLibJS. It simply adds the constraint to the physics system.

However, since these constraints are simply bound to a point in the world (this is where using JConstraintMaxDistance would have been much simpler), you have to manually move each point that each square is bound to. Luckily, I’d previous solved this little puzzle back when I was doing relative animation.

That takes place within the animation loop and simply iterates over each constraint and moves it according to the orientation of the three.js representation of the panel. If it all goes according to plan, it should look something like this when spun.

Yeah, it doesn’t look like they’re on ropes, but hey, it’s a lot closer than I was a few days ago.

View the demo (requires an HTML5-capable browser). You can use the up and down arrow keys to move the camera and click the squares to add and remove their respective JigLibJS constraints. The panel also auto-aligns every five seconds, so don’t freak out when things move without you doing anything.

• 3D rendering
• HTML5
• HTML5 Canvas
• JigLibJS
• physics engine
• three.js